Logistic回归

对于分类器我们想要的函数应该是，能接受所有的输入然后预测出类别。例如，在两个类的情况下，上诉函数输出0或1。 这种函数称为 海维赛德阶跃函数(Heaviside step function)或单位阶跃函数。
然而，海维赛德阶跃函数在跳跃点上从0瞬间跳跃到1。这个瞬间跳跃过程有时很难处理。
幸好，另一个函数也有类似的性质，且数学上更易处理，这就是Sigmoid函数。
Sigmoid函数具体的计算公式如下：

$$\sigma(z)=\frac{1}{1+e^{-z}}$$

下图就是Sigmoid函数曲线

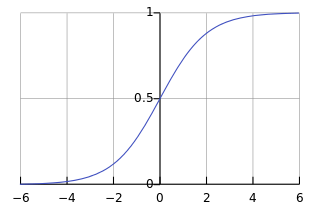
如果横坐标刻度足够大，Sigmoid函数看起来很想一个阶跃函数。
因此，为了实现Logistic回归分类器，我们可以在每个特征上乘以一个回归系数，然后吧所有的结果相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0～1之间的数值。任何大于0.5的数据被分入1类，小于0.5被分入0类。所以，Logistic回归也可以被看成是一种概率估计。

现在我们的问题就变成了：最佳回归系数是多少？如何确定它们的大小？

###确定最佳回归系数
Sigmoid函数的输入记为 $z$ ，由下面公式得出：

$$z = w_0x_0 + w_1x_1 + w_2x_2 + \dots + w_nx_n$$

也就是：

$$z = w^Tx$$

其中 $x$ 是分类器的输入数据，向量 $w$ 是我们要找的最佳系数。
下面我们使用梯度下降方法来求得最佳系数。

####梯度下降
要使用梯度下降方法我们就得有一个凸的损失函数来保证下降所求的的最小值是全局最小值。
所以我们给Sigmoid函数选定的损失函数为：

$$Cost(h_\theta(x), y) = \left\{ \begin{array}{l} \ \ \ \ \ -log(h_\theta(x))\ \ \ if\ y = 1 \\ -log(1 - h_\theta(x)) \ \ \ if\ y = 0 \end{array} \right.$$

由于 $y = 0\ or\ 1$我们的损失函数就化为：

$Cost(h_\theta(x), y) = -ylog(h_\theta(x)) - (1 - y)log(h_\theta(x))$
所以：

$$J(\theta) = -\frac{1}{m}\left[\sum_{i=1}^{m}y^{(i)}logh_\theta(x^{(i)} + (1 - y^{(i)})log(1 - h_\theta(x^{(i)}))\right]$$

由于

$$\log h_\theta(x^i)=\log\frac{1}{1+e^{-\theta x^i} }=-\log ( 1+e^{-\theta x^i} ),$$ $$\log(1- h_\theta(x^i))=\log(1-\frac{1}{1+e^{-\theta x^i} })=\log (e^{-\theta x^i} )-\log ( 1+e^{-\theta x^i} )=-\theta x^i-\log ( 1+e^{-\theta x^i} ),$$

所以

$$J(\theta)=-\frac{1}{m}\sum_{i=1}^m \left[y_i\theta x^i-\theta x^i-\log(1+e^{-\theta x^i})\right]=-\frac{1}{m}\sum_{i=1}^m \left[y_i\theta x^i-\log(1+e^{\theta x^i})\right],~~(*)$$

又由于

$$-\theta x^i-\log(1+e^{-\theta x^i})= -\left[ \log e^{\theta x^i}+ \log(1+e^{-\theta x^i} ) \right]=-\log(1+e^{\theta x^i}).$$

所以我们计算$(*)$ 的偏导数是就有：

$$\frac{\partial}{\partial \theta_j}y_i\theta x^i=y_ix^i_j,$$ $$\frac{\partial}{\partial \theta_j}\log(1+e^{\theta x^i})=\frac{x^i_je^{\theta x^i}}{1+e^{\theta x^i}}=x^i_jh_\theta(x^i),$$

于是我们有

$$\theta_j := \theta_j - \alpha\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$

除了梯度下降方法我们还可以使用
1. 共轭梯度法(Conjugate gradient)
2. BFGS
3. L-BFGS

这些方法的优势是不需要人工去选择 $\alpha$ ,大多数情况下会比梯度下降快。